Robust Stability of Neural Network Control Systems with Interval Matrix Uncertainties
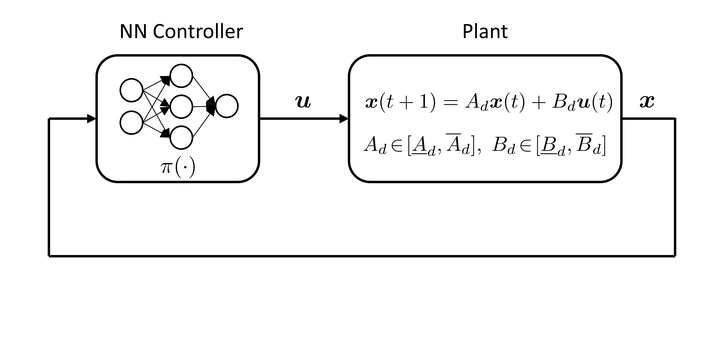 Feedback system that contains a plant with interval matrix uncertainties and NN controller
Feedback system that contains a plant with interval matrix uncertainties and NN controllerAbstract
Neural networks have become increasingly popular in controller design due to their versatility and efficiency. However, their integration into feedback systems can pose stability challenges, particularly in the presence of uncertainties. This work addresses the problem of certifying robust stability in neural network control systems with interval matrix uncertainties. Leveraging classical robust stability techniques and the quadratic constraint-based method to characterize the input–output behavior of neural networks, we derive novel robust stability certificates formulated as linear matrix inequalities. To reduce computational complexity, we introduce three relaxed sufficient conditions and establish their equivalence in terms of feasibility. Additionally, we explore their connections to existing robust stability results. The effectiveness of the proposed approach is demonstrated through inverted pendulum and mass–spring–damper examples.
Type
Publication
Automatica